Trading VXX with nearest neighbors prediction
An experienced trader knows what behavior to expect from the market based on a set of indicators and their interpretation. The latter is often done based on his memory or some kind of model. Finding a good set of indicators and processing their information poses a big challenge. First, one needs to understand what factors are correlated to future prices. Data that does not have any predictive quality only intorduces noise and complexity, decreasing strategy performance. Finding good indicators is a science on its own, often requiring deep understandig of the market dynamics. This part of strategy design can not be easily automated. Luckily, once a good set of indicators has been found, the traders memory and 'intuition' can be easily replaced with a statistical model, which will likely to perform much better as computers do have flawless memory and can make perfect statistical estimations.
Regarding volatility trading, it took me quite some time to understand what influences its movements. In particular, I'm interested in variables that predict future returns of VXX and XIV. I will not go into full-length explanation here, but just present a conclusion : my two most valuable indicators for volatility are the term structure slope and current volatility premium.
My definition of these two is:
The indicators for the same period are plotted below:
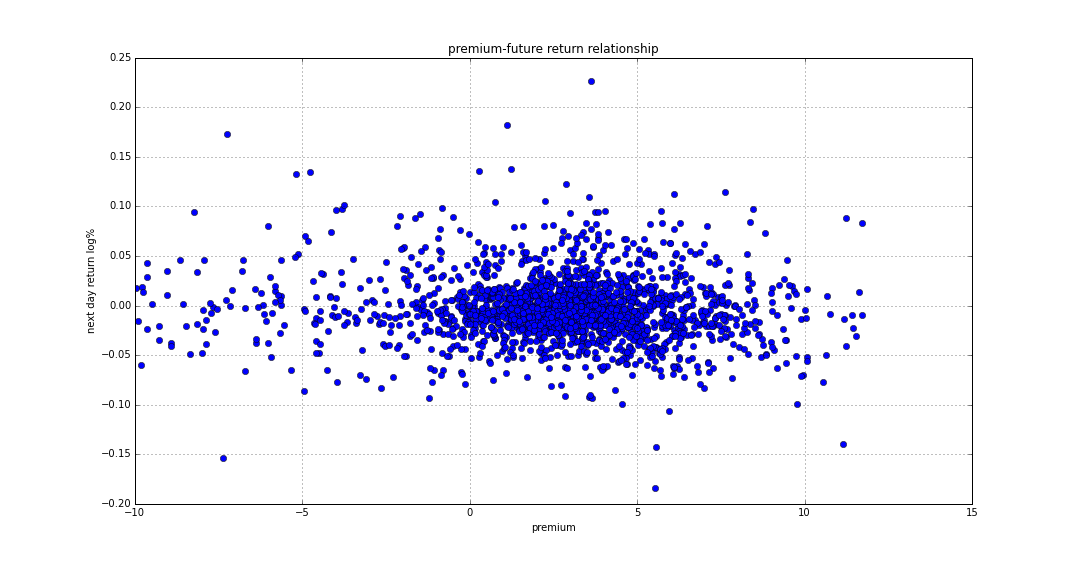
If we take one of the indicators (premium in this case) and plot it against future returns of VXX, some correlation can be seen, but the data is extremely noisy:
Still, it is clear that negative premium is likely to have positive VXX returns on the next day.
Combining both premium and delta into one model has been a challenge for me, but I always wanted to do a statistical approximation. In essence, for a combination of (delta,premium), I'd like to find all historic values that are closest to the current values and make an estimation of the future returns based on them. A couple of times I've started writing my own nearest-neighbor interpolation algorithms, but every time I had to give up... until I came across the scikit nearest neighbors regression. It enabled me to quickly build a predictor based on two inputs and the results are so good, that I'm a bit worried that I've made a mistake somewhere...
Here is what I did:
In the last two plots, the strategy seems to perform the same in- and out-of-sample. Sharpe ratio is around 2.3.
I'm very pleased with the results and have the feeling that I've only been scratching the surface of what is possible with this technique.
Regarding volatility trading, it took me quite some time to understand what influences its movements. In particular, I'm interested in variables that predict future returns of VXX and XIV. I will not go into full-length explanation here, but just present a conclusion : my two most valuable indicators for volatility are the term structure slope and current volatility premium.
My definition of these two is:
- volatility premium = VIX-realizedVol
- delta (term structure slope) = VIX-VXV
VIX & VXV are the forward 1 and 3 month implied volatilities of the S&P 500. realizedVol here is a 10-day realized volatility of SPY, calculated with Yang-Zhang formula. delta has been often discussed on VixAndMore blog, while premium is well-known from option trading.
It makes sense to go short volatility when premium is high and futures are in contango (delta < 0). This will cause a tailwind from both the premium and daily roll along the term structure in VXX. But this is just a rough estimation. A good trading strategy would combine information from bothpremium and delta to come with a prediction on trading direction in VXX.
I've been struggling for a very long time to come up with a good way to combine the noisy data from both indicators. I've tried most of the 'standard' approaches, like linear regression, writing a bunch of 'if-thens' , but all with a very minor improvements compared to using only one indicator. A good example of such 'single indicator' strategy with simple rules can be found onTradingTheOdds blog . Does not look bad, but what can be done with multiple indicators?
I'll start with some out-of-sample VXX data that I got from MarketSci. Note that this is simulated data, before VXX was created.
If we take one of the indicators (premium in this case) and plot it against future returns of VXX, some correlation can be seen, but the data is extremely noisy:
Still, it is clear that negative premium is likely to have positive VXX returns on the next day.
Combining both premium and delta into one model has been a challenge for me, but I always wanted to do a statistical approximation. In essence, for a combination of (delta,premium), I'd like to find all historic values that are closest to the current values and make an estimation of the future returns based on them. A couple of times I've started writing my own nearest-neighbor interpolation algorithms, but every time I had to give up... until I came across the scikit nearest neighbors regression. It enabled me to quickly build a predictor based on two inputs and the results are so good, that I'm a bit worried that I've made a mistake somewhere...
Here is what I did:
- create a dataset of [delta,premium] -> [VXX next day return] (in-of-sample)
- create a nearest-neighbor predictor based on the dataset above
- trade strategy (out-of-sample) with the rules:
- go long if predicted return > 0
- go short if predicted return <0
The strategy could not be simpler...
The results seem extremely good and get better when more neigbors are used for estimation.
First, with 10 points, the strategy is excellent in-sample, but is flat out-of-sample (red line in figure below is the last point in-sample)
Then, performance gets better with 40 and 80 points:
In the last two plots, the strategy seems to perform the same in- and out-of-sample. Sharpe ratio is around 2.3.
I'm very pleased with the results and have the feeling that I've only been scratching the surface of what is possible with this technique.
'Data Mining & R' 카테고리의 다른 글
| Algorithmic trading with Python (0) | 2016.05.10 |
|---|---|
| quantiacs : algorithmic trading competition (0) | 2016.05.10 |
| Backtesting with TWP backtesting module (0) | 2016.05.10 |
| AN INTRODUCTION TO BACKTESTING WITH PYTHON AND PANDAS (0) | 2016.05.09 |
| 오피니언마이닝에 기반한 주식 매매 시그널 - opinion mining, social mining (0) | 2016.05.04 |