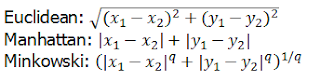http://chapter5k.blogspot.kr/2016/01/knnk-nearest-neighbors-r.html
kNN(k Nearest Neighbors) 알고리즘 소개 및 R 구현
이번 주는 분류에 대한 최근접 알고리즘 접근법인 kNN 알고리즘을 간략하게 공부했다.
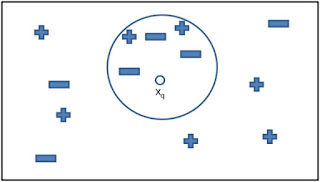
kNN알고리즘은 범주를 알지 못하는 데이터가 있을 때, 근접한 k개의 데이터를 이용해 범주를 지정해주는 역할이다.
쓰임새는,
이미지나 비디오에서 얼굴과 글자를 인식하는 컴퓨터 비전 애플리케이션
개인별 추천 영화 예측
특정 단백질과 질병을 추출하는 데 사용하는 유전자 데이터의 패턴 식별
등 다양하다.
이러한 kNN알고리즘의 장단점은 아래와 같다.
- 거리계산
kNN알고리즘은 최근점 이웃의 거리를 계산하는 다양한 방법이 있다. 대표적으로 유클리디언 거리를 사용한다.
- k의 선택
또한 몇 개의 근접이웃 k를 결정하는 문제도 중요하다. 보통 k의 선택은 학습해야 할 개념의 난이도와 훈련 데이터의 개수에 달려있으며, 일반적으로 훈련 데이터의 개수에 제곱근으로 설정한다. 또한, 훈련 데이터의 개수에 제곱근으로 설정하기도 한다.
만약 k를 너무 크게 설정하면 주변에 있는 데이터와 근접성이 떨어지게 되어 클러스터링이 잘 되지 않고, 너무 작게하면 노이지 데이터나 이상치와 이웃이 될 가능성이 있으므로 이러한 문제들을 피할 수 있도록 적절한 k의 선택이 필요하다.
- kNN R function.
R에서는 다양한 kNN패키지가 있으며 가장 기본적인 패키지는 class 패키지로 이용할 수 있다. 하지만 직접 구현해보며 알고리즘을 익히는 것이 목표이기에 직접 코딩을 하고자 한다.
- kNN in R programming.
패키지의 결과와 생성 함수의 결과가 같읕 것으로 보아 성공적으로 코딩하였다.
kNN알고리즘은 범주를 알지 못하는 데이터가 있을 때, 근접한 k개의 데이터를 이용해 범주를 지정해주는 역할이다.
쓰임새는,
이미지나 비디오에서 얼굴과 글자를 인식하는 컴퓨터 비전 애플리케이션
개인별 추천 영화 예측
특정 단백질과 질병을 추출하는 데 사용하는 유전자 데이터의 패턴 식별
등 다양하다.
이러한 kNN알고리즘의 장단점은 아래와 같다.
장점 | 단점 |
- 단순하며 효율적 - 데이터 분산에 대한 추정을 만들 필요가 없음 - 빠른 훈련 단계 | - 모델을 생성하지 않음 - 느린 분류 단계 - 많은 메모리가 필요 - 명목형 속성과 결측 데이터는 추가적인 처리 필요 |
- 거리계산
kNN알고리즘은 최근점 이웃의 거리를 계산하는 다양한 방법이 있다. 대표적으로 유클리디언 거리를 사용한다.
- k의 선택
또한 몇 개의 근접이웃 k를 결정하는 문제도 중요하다. 보통 k의 선택은 학습해야 할 개념의 난이도와 훈련 데이터의 개수에 달려있으며, 일반적으로 훈련 데이터의 개수에 제곱근으로 설정한다. 또한, 훈련 데이터의 개수에 제곱근으로 설정하기도 한다.
만약 k를 너무 크게 설정하면 주변에 있는 데이터와 근접성이 떨어지게 되어 클러스터링이 잘 되지 않고, 너무 작게하면 노이지 데이터나 이상치와 이웃이 될 가능성이 있으므로 이러한 문제들을 피할 수 있도록 적절한 k의 선택이 필요하다.
- kNN R function.
R에서는 다양한 kNN패키지가 있으며 가장 기본적인 패키지는 class 패키지로 이용할 수 있다. 하지만 직접 구현해보며 알고리즘을 익히는 것이 목표이기에 직접 코딩을 하고자 한다.
- kNN in R programming.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | normalize <- function(x) {num <- x - min(x)denom <- max(x) - min(x)return (num/denom)}## 해당 방식으로 normalize 사용 가능iris_norm <- as.data.frame(lapply(iris[1:4], normalize))## set.seed는 난수를 재현 가능하도록, 난수 패턴을 저장해놓는 것set.seed(1234)## traning data와 test data를 0.67, 0.33의 확률로 나누기 위한 샘플 생성ind <- sample(2, nrow(iris), replace=TRUE, prob=c(0.67, 0.33))## 수치 데이터와 수치 데이터의 Label 을 따로 정의iris.training <- iris[ind==1, 1:4]iris.test <- iris[ind==2, 1:4]iris.trainLabels <- iris[ind==1, 5]iris.testLabels <- iris[ind==2, 5]## knn 함수 생성knn.t <- function(train, test, cl, k){test.result <- numeric(length(test))## 유클리디언 거리 함수euclidean.distance <- function(x1, x2) sqrt(sum((x1-x2)^2))## 전체 데이터에 유클리디언 거리를 계산for(i in 1:nrow(test)){train$dist=sapply(1:nrow(train), function(ntrain){ euclidean.distance(train[ntrain,1:4], test[i,1:4]) })## 가장 가까운 k개의 데이터 위치를 저장nearest.k=order(train$dist)[1:k]## train data에서 해당 하는 위치의 라벨을 저장nearest.k.categories=cl[nearest.k]## k개 중 가장 많이 나온 라벨을 저장common.category=names(sort(table(nearest.k.categories),decreasing=TRUE)[1])## 결과값(라벨들)을 저장test.result[i]=common.category}train$dist=NULLtest.result}## 실험result <- knn.t(train=iris.training, test=iris.test, cl=iris.trainLabels, k=3)result## gmodels 패키지를 통해 예측률 확인library(gmodels)CrossTable(x=iris.testLabels, y=result, prop.chisq=FALSE) |
1 2 3 4 5 6 7 | ## class패키지의 knn 함수를 통해 결과 비교library(class)iris_pred <- knn(train=iris.training, test=iris.test, cl=iris.trainLabels, k=3)iris_predCrossTable(x=iris.testLabels, y=iris_pred, prop.chisq=FALSE) |
패키지의 결과와 생성 함수의 결과가 같읕 것으로 보아 성공적으로 코딩하였다.
'Data Mining & R' 카테고리의 다른 글
| Digit Classification Using HOG Features (0) | 2017.03.31 |
|---|---|
| Classification in the Presence of Missing Data (0) | 2017.03.31 |
| Supervised Learning, Unsupervised Learning (0) | 2017.03.13 |
| 데이터마이닝 소개와 분석 방법 (LG CNS) (0) | 2017.03.09 |
| DataMining의 기법 (0) | 2017.03.02 |